One Group, Zero Covariates (OSGM)
This models the input as a simple mean (one group), so it is sometimes referred to as a "One-Sample Group Mean" or OSGM. It is simply designed to test whether the mean of the input is 0. This is not very useful for a thickness study because the mean thickness should never be 0, but can be useful in fMRI, where the mean hemodynamic response amplitude can be 0. Everything is the same for DODS and DOSS.
FSGD File (g1v0.fsgd)
GroupDescriptorFile 1 Title OSGM Class Main Input subject1 Main Input subject2 Main
Nclasses = 1
Nvariables = 0
Regressors
NregressorsDODS = Nclasses*(Nvariables+1) = 1*(0+1) = 1
NregressorsDOSS = Nclassesd + Nvariables = 1+0 = 1
Regressor1: All ones. Codes mean/offset for Main
Contrasts
The number of columns in each contrast matrix must be the same as the number of regressors (Nregressors). If there is only one row in the contrast matrix, then the result will be a t-test and will have a sign. Reversing the signs in the contrast matrix will only change the sign of the output, not its magnitude. If there is more than one row, the result will be an F-test and will be unsigned.
Contrast 1 (intercept.mtx)
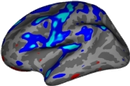
Null Hypothesis: is the intercept/mean equal to 0? Note: This is the only contrast that can be tested with this design.
1
This is a t-test with the intercept>0 being positive (red/yellow).
mri_glmfit command
This is an example invocation of mri_glmfit. Depending upon your application, you may have other options as well.
mri_glmfit \ --glmdir g1v0 \ --y y.mgh \ --fsgd g1v0.fsgd \ --C intercept.mtx